Galileo's Proposed Authentication Algorithm: Part 1
Position, velocity and time (PVT) information can be a ’nice to have’, but in other circumstances knowing place and time has legal or military importance as well. Heavy vehicles for example are typically outfitted with tachographs that track driver speed and/or location. This has importance for rest regulations, but also to check if loads are actually from where they say they are.
Our Global Navigation Satellite Systems so far are broadcasting unauthenticated data, at least to civilian users. Or in other words, a satellite sends us information, but we have no way to determine if the messages are really coming from GPS, GLONASS, Galileo or BeiDou.
The subject of PVT spoofing (prevention) is vast and the problem is real. There are no easy solutions and it is easy to get bogged down in finding downsides to whatever is suggested to improve things.
Adding authentication and integrity to GNSS messages is definitely one part of any solution though, but it should be realised that satellites are not sending us our position directly. They are sending us data that allows us to determine our position, velocity and time. Even if all messages have perfect integrity, a sophisticated attacker could do RF tricks to make a receiver think it is somewhere (or somewhen!) else.
Nevertheless, being able to trust messages we receive is a very important step. Galileo will soon pioneer in this respect by enabling Open Service Network Message Authentication (OSNMA).
In this post (which is part 1 of a series), I hope to explain the rather interesting cryptography (“Timed Efficient Stream Loss-Tolerant Authentication” aka “TESLA”) that is being proposed for OSNMA.
In order to keep things comprehensible, I focus only on commonly used Galileo modes. In addition, I’ll cover enough cryptography to give a real insight into how things work, but gladly refer to RFC 4082 and the Galileo draft OSNMA specification for the full details.
UPDATE! The official description is now live on the Galileo Service Centre page
In this part 1, there are some significant simplifications of Galileo specific bits, but rest assured that in part 2 we’ll get down to the details of the actual implementation. In part 3 we’ll address the really tricky areas (like key rollover) and perhaps open problems. Finally, part 4 will touch on the generic problem of GNSS spoofing & jamming.
But before we start - I need to thank the many people that volunteer to read drafts of my posts before I put them online. If these posts look in any way professional or well-informed, this is in large part because of the help from Twitter friends, the Galileo IRC (chat) channel or unnamed Galileo professionals willing to lend me their expertise. Thanks!
The challenge
Galileo Satellites send out a message exactly once every two seconds. Many of these messages actually get lost (“packet loss”), but that’s ok, they are part of a carousel that repeats every 30 seconds, and not all messages are required for PVT. For Galileo, a set of messages will typically rotate for around 10 minutes, and then be replaced by a new set. Every satellite has its own unique set of messages.
Here is an idea of what such messages look like, per satellite:
1: Atomic clock is ahead by 1.234 ns, drifting by 12 ps/s
2: Orbital radius is 22000km, eccentricity is 1.000034, ...
3: Whole bunch of orbital parameters
4: Yet more orbital parameters
5: Galileo Week Number, number of leap seconds, seconds since Sunday
6: News about other satellites in the fleet
7: Yet more news about the other satellites
8: Information about the ionosphere
9: NOP
...
For Galileo, the content of every message is 128 bits in size. In addition, there are 24 CRC bits, further bits for Search and Rescue data, some overhead, plus 40+8+2 bits of reserved space, for a total of 240 bits per message. Anything we do in terms of authentication has to fit in the reserved space.
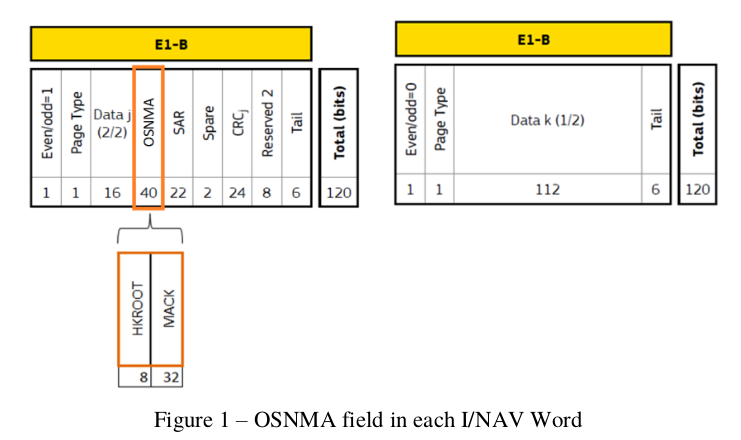
Message layout
Now, the naive way to get authentication is to use public key encryption and sign each message individually. One problem with this idea is that modern receivers listen to many satellites at the same time, and on multiple frequency bands as well. It is entirely possible that a receiver would need to verify 20 signatures per second.
And that is where we hit the first problem - the embedded CPUs in many receivers would struggle to perform that much public key cryptography. They might also use more battery power than we’d like them to.
In addition, even the smallest elliptic curve digital signatures weigh in at hundreds of bits - and there simply isn’t that much room available on the satellite RF channel - we only have around 40 bits (per message). The whole navigation message itself is smaller than a typical ECDSA signature!
So, straight (elliptic curve) public key cryptography is out.
Could we be clever? Perhaps take the whole carousel of messages, and lavish one public cryptography operation on the whole set? We could, but since individual messages frequently get lost, this would effectively make verification impossible - it is rare for a complete set of 15 messages to arrive unscathed.
The symmetric trick
We could of course add a simple MAC signature to each message. To verify the MAC, the receiver would need to know the (symmetric!) key that is used. This would work, but it would also be terrible - if a receiver had that key (for verification purposes), it could simply impersonate the whole satellite system! When doing “symmetric authentication”, the verification and signing keys are identical.
Still, this is what is proposed, but with a twist. Every individual message carries an indicator that says by which key id it is signed, plus a MAC made with that key.
And here is the twist: that key is only transmitted AFTER the message has been received.
To make this work, a receiver parks (but does not use) messages it receives, until the associated key is sent out, and can verify that the data received earlier was in fact signed correctly.
This introduces an element of asymmetry - at first only the sender has access to the key, and only the sender can generate signatures. After disclosure, receivers can verify the authenticity for any messages they received BEFORE the key was shared.
(if this isn’t entirely clear yet, there is a recap in the next section).
Now, this is pretty clever, but there are a lot of issues. Like, how do we trust the key we just received?
Trust
So far, we know that if we think the latest key we received is authentic, we can verify the signatures on the previous messages, and extend that trust backwards.
So, we get:
...
Message 2 signed with key id 5
Message 3 signed with key id 5
Message 4 signed with key id 5
...
Message 15 signed with key id 5
Message 1: key 5 was 0x23543542343
Message 2, signed with key id 6
Message 3, signed with key id 6
After this sequence, we can verify all the messages signed with key 5, and trust them as much as we trust key 5. Which is to say, not at all.
(Note that in reality, the whole new key does not suddenly appear in one message - stay tuned for part 2 of this series to learn how this really works).
Key chains
This is where it gets clever. Every once in a while, Galileo will send out a key with a real public key signature on it. The “Galileo public key” is published widely, so we know we can trust it. We can’t do such public key signatures very often though - there isn’t enough bandwidth, CPU and battery power available. But every once in a while we can do it.
Ok, so once we have verified the public key signature, we can trust (say) key id 0. This is nice and all, but it does nothing for our trust of key id 5. What we need is a trust chain.
To create such a chain, keys are actually generated using the “next” key as input. Put very simply (and incorrectly), key id 5 is sorta the hash of key id 6, key id 4 can be derived from key id 5 etc.
In other words, if you know key 6, you can derive keys 5, 4, 3, 2, 1 and ultimately 0. And you can then check the validity of key 0 with the real public key signature!
So to validate a message, a receiver waits until it sees the key a message was signed with. If this is key id 6, it will also calculate keys 5, 4, 3, 2, 1 and 0. It will then check if a real public key signature of key id 0 is on file. And if all these things match, we might decide to trust the messages signed with those keys.
Summarising
By signing messages with a key that is briefly secret, and disclosing it after some delay, receivers can verify if earlier messages were signed correctly with that key.
Keys are generated by designing them in a chain so that each key can be used to derive a previous key. And occasionally, Galileo signs a key using actual public key cryptography, and by reasoning backwards, we can validate that every key stems from the original signed ‘anchor’.
With these two techniques, it is indeed possible to create small symmetric signatures that nevertheless enable message authentication.
Further details
Now, as with all cryptography, details matter a lot. It is very important that a receiver does not use a key that was transmitted for verification of messages that come in later.
There are important choices to be made in TESLA on which algorithms to support for signatures, key derivation and public key operations. In addition, choices must be made on the length of key chains and how long a key is used for. If this is too long for example, a receiver will lag behind in processing data.
In addition, it is of course abundantly clear that OSNMA only works if the receiver and transmitter agree on what time it is. Many attacks on TESLA revolve around this problem.
In part two of this post, where I delve into what Galileo-specific choices have been made for the TESLA protocol, and how keys actually get distributed. Suggestions, corrections and questions are very welcome on bert@hubertnet.nl or via Twitter, @GalileoSats.
