Improved Galileo Time to First Fix
In the world of Global Navigation Satellite Systems (GNSS), change tends to happen very slowly and cautiously. It is therefore quite exciting how many new features Galileo, the “European GPS” has been rolling out lately.
Earlier I wrote a little bit about the High Accuracy Service (HAS), whereby the Galileo satellites themselves provide properly equipped receivers (not your phone) with near-realtime updates that can be used to achieve very good accuracy. I also wrote a series on OSNMA, the rather special Galileo message authentication protocol.
Recently three further new features have appeared that can be received by the hardware already found in the billions of phones that support Galileo. The goal is to get you to a ‘fix’ of time and place faster and more robustly. To do so, Galileo satellites now deploy some rather clever maths and tricks.
These are especially useful for unconnected devices (without ‘assisted GPS’), but the new features also provide resilience in case of disrupted communications, for example during disasters. In addition, even well connected devices can speed up their time synchronisation, which in turn speeds up the time to first fix.
Getting a fix
As I noted in a recent presentation on GPS, BeiDou, Galileo and GLONASS, GNSS in essence consists of over one hundred satellites beeping at you every 1.0000000000 seconds. If you know exactly where those satellites are, and how their clocks are doing, the relative arrival times of those beeps can tell you where you are (and what time it is).
In the very old days, a GPS receiver could easily take 15 minutes to get a fix. Many of those minutes would be spent merely finding the satellite radio signals. Modern chips can do this very quickly, but then we’re not yet done.
The satellites broadcast messages (or ‘words’), and multiple of those messages are required to precisely establish the satellite’s orbit and clock characteristics. Since GNSS transmissions are really low power, for Galileo this could take 30 seconds given perfect conditions. However, conditions rarely are perfect - if an important message is missed or too garbled, we have to wait 30 seconds for the next transmission.
For this reason, most phones attempt to download the orbit and clock details from the cloud. This allows them to immediately use the timing of the beeps to figure out where you are. Now, this is pretty nice, but it only works if you have connectivity and if this “assisted GPS” is working correctly.
Galileo Improved INAV
The European Commission set the goal to speed up the Galileo ’time to first fix’ without cloud assistance. As noted, Galileo broadcasts a carousel of messages, and this carousel (mostly) repeats every 30 seconds. Each message takes 2 seconds, so there are 15 ‘slots’. The satellite ephemeris (orbit) and clock details are spread out over 4 messages.
Given typical reception conditions however, we need to be pretty lucky to receive all four messages perfectly in just one rotation.
The good news is that lots of the 15 slots in the carousel were in fact empty, which meant there were options for change.
To speed up the time to first fix, three measures have been implemented:
- Broadcast a new lower precision short term orbit/clock description message (word 16)
- Broadcast 4 new messages that provide Reed-Solomon parity bits to protect the 4 existing ephemeris messages. This is construed that any four out of the now 8 messages suffice to reconstruct the full ephemeris and clock (words 17, 18, 19 and 20)
- Wiggle some bits so every Galileo message tells you the Galileo System Time modulo 6 seconds, even without decoding the message
Orbit and clock models
From the ground the orbits and clocks of the satellites are monitored carefully. In addition, the earth’s gravitational field, the influence of the sun and the moon are all well known. There are also models of the influence of solar wind. On the ground, there is enough data to predict the orbit of a satellite perhaps 24 hours ahead of time. Roughly the same thing holds for the clock, as long as the clock behaves (which is often not the case).
A full Galileo ephemeris (orbit)/clock description is around 500 bits in size and contains enough information to model things for around 4 hours. On the ground, there is knowledge to calculate several such 500 bit descriptors ahead of time, and these are continuously uplinked, so that a satellite (in theory) could go without ground communications for 24 hours.
It is also possible to create far smaller ephemeris/clock descriptors that have far briefer predictive abilities, and this is what we find in new Galileo message type 16.
The word contains a 122 bit descriptor with an intended validity of 10 minutes. It gets broadcast twice in the 30 second carousel, so on average a receiver should see it after around 8 seconds (and 95% of the time within 15 seconds).
Although it is valid for 10 minutes, a fresh version of this descriptor gets broadcast every 30 seconds.
Even with the reduced validity period, there is only so much information you can cram in 122 bits, so a position derived from this reduced accuracy message will be less precise. In this paper we can read that the range established from the reduced precision ephemeris should be 3 meters less precise.
Technically speaking, the designers of this message have cleverly created a mapping from the reduced accuracy ephemeris parameters to the ‘regular’ ephemeris parameters. This means receivers can reuse their existing math to do orbit calculations.
I spent a good few hours getting this to work, and perhaps the following code snippet can serve as inspiration:
uint32_t getT0e(){ return d_t0r; }
static constexpr double Anominal{29600000.0};
double getSqrtA(){ return sqrt(Anominal + ldexp(1.0*d_gm.deltaAred, 8)); }
double getE(){ return ldexp(sqrt(d_gm.exred*d_gm.exred + d_gm.eyred*d_gm.eyred),
-22); }
double getCuc() { return 0; } // radians
double getCus() { return 0; } // radians
double getCrc() { return 0; } // meters
double getCrs() { return 0; } // meters
double getM0() { return ldexp(M_PI * d_gm.lambda0red, -22) -
getOmega(); }
double getDeltan() { return 0; } //radians/s
static constexpr double iNominal{56.0};
double getI0() { return M_PI*iNominal/180.0 +
ldexp(d_gm.deltai0red * M_PI, -22); }
double getCic() { return 0; } // radians
double getCis() { return 0; } // radians
double getOmegadot() { return 0; } // radians/s
double getOmega0() { return ldexp(d_gm.omega0red * M_PI, -22); }
double getIdot() { return 0; } // radians/s
double getOmega() { return atan2(d_gm.eyred, d_gm.exred); }
// pair of nanosecond, nanosecond/s
std::pair<double, double> getAtomicOffset(int tow) const
{
int delta = ephAge(tow, d_t0r);
// 2^-26 2^-35
double cur = d_gm.af0red + ldexp(1.0*delta*d_gm.af1red, -9);
double trend = ldexp(d_gm.af1red, -9);
// now in units of 2^-26 seconds, which are ~14.9 nsec each
double factor = ldexp(1000000000.0, -26);
return {factor * cur, factor * trend};
}
Of special note, the getE() function attempts to get the most out of the floating point precision. If you do the ldexp() inside the sqrt() you might get some very small numbers. Additionally, although the Galileo OSS ICD 2.0 is quite clear, you might miss that you have to transpose ω as well and not use the ω provided by the normal Galileo ephemeris.
This brings me to a further point. The goal of an ephemeris descriptor is to enable you to perform the most accurate range measurement to the satellite. To do so, the supplied parameters allow you to predict the satellite’s orbit and clock offset. But even though the ephemeris parameters look a lot like physical orbital elements that Johannes Kepler would recognize, this is not what the parameters are. The parameters of even the full precision ephemeris are optimized to give you good results. They are not measurements of the satellite’s actual orbit.
Now, although this is technically true, for the full precision ephemeris, it is somewhat of a philosophical point. The parameters of the full precision ephemeris in fact do correspond closely to what is physically happening. But technically speaking, this need not be the case.
For the reduced precision ephemeris, this is DEFINITELY not the case. The orbital software does its best to create a description that when fed to the normal orbital algorithm delivers something that allows you to determine the range as best as possible over the next 10 minutes. To this end, the software wiggles the 122 bits of parameters to get the best fit. Two parameters that perhaps unexpectedly get wiggled are af0red and af1red, which notionally describe how far the atomic clock is ahead of Galileo System Time, and the rate at which the clock drifts.
In this case, these parameters are tweaked to provide around 100 meters of range corrections. By artificially making the clock appear to be ahead/behind by up to a microsecond, a receiver will conclude the satellite is further away or closer than it would otherwise be. This correction improves the range calculation.
The Galileo SIS ICD documents are very clear that the parameters from the reduced precision ephemeris should never be mixed with those from the full precision version. They also remind you to take the satellite clock into account. So to be clear, the ICD is correct, and if you follow its instructions, you’ll get a working receiver.
But if you take the reduced ephemeris and compare it to the full ephemeris, you’ll find 100 meter errors, until you project the calculated ECEF position of the satellite out by the calculated clock offsets, which as noted can differ by a microsecond (!).
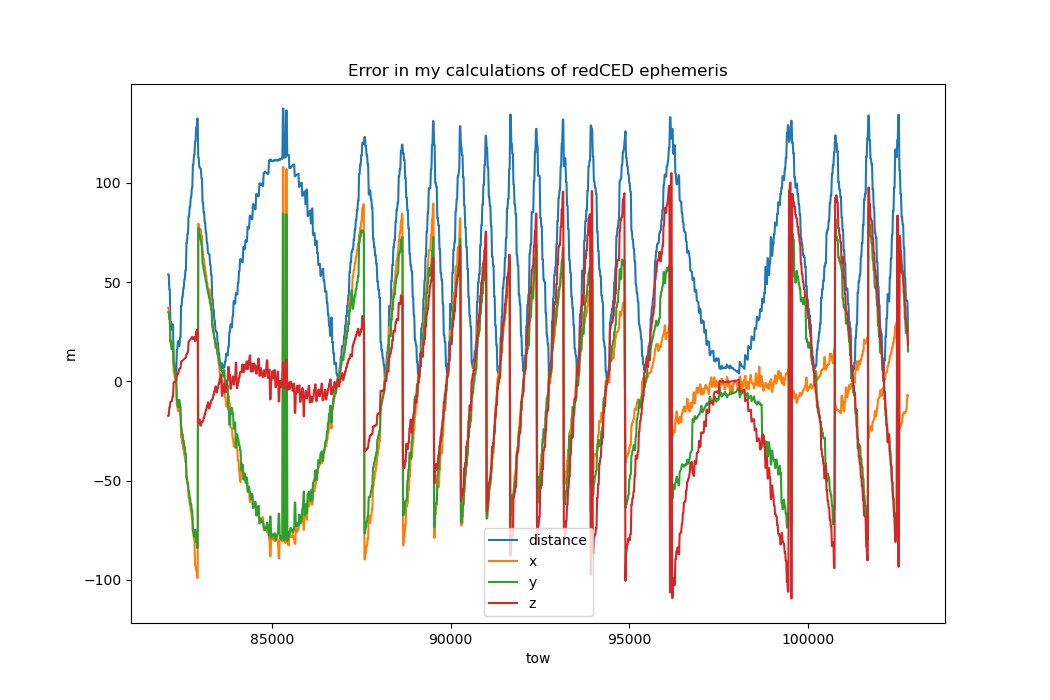
Pretty graph showing the error you get if you neglect af0red and af1red
So the key is - when relying on the reduced precision ephemeris, use ONLY parameters actually part of that reduced ephemeris, but do use all of them (including af0red and af1red). Once the full precision variant arrives, use nothing but that.
I’m much indebted to Cillian O’Driscoll, Daniel Estévez and Matteo Paonni who helped me figure out why my numbers were off so much, and pointing me towards the clock parameters!
Parity protection
In the 30 second sub-frame, containing 15 messages, 2 slots have been dedicated to broadcasting parity bits for the 4 existing ephemeris messages. The clever way in which this has been done means that any 4 out of the now 8 ephemeris messages are sufficient to recover full orbit and clock data.
The four new parity words (17, 18, 19, 20) share two slots in the 30 second carousel. This means that in the one minute it takes to broadcast two sub-frames, a receiver will have seen 8 copies of the ephemeris words (words 1, 2, 3 and 4), and 4 copies of the parity words.
Messages often arrive slightly garbled, which is then detected because the CRC check fails. Traditionally, such messages had to be discarded. But given the many parity bits available now, such messages can now be corrected and contribute to a complete ephemeris.
To make this happen, the designers of the new messages used the rather miraculous Reed-Solomon algorithm, which I wrote about earlier. R-S takes a message and adds parity bits to it. But the beauty of the thing is that the algorithm can repair damage in any place it occurs - even if this happens in the parity bits itself.
Quoting from the earlier post:
In short, Reed-Solomon is a cool way to protect messages against damage or partial arrival. At your choice, you can add t parity symbols to a message.
These t parity symbols then allow you to:
- recover from t/2 corrupted symbols in unknown places
- recover from t corrupted/missing symbols in known places
- detect that the message was damaged (unless there are more than t corruptions)
A symbol can be 8 bits long and equal a byte, but this does not have to be the case.
Not only is this is pretty good error resilience, it provably does not get any better than this (at least, not on a per symbol basis).
You can pick t at will, which means you can choose the level of protection you want.
What you can’t pick at will however is the length of the resulting protected block: this is always 255 bytes (when using byte-sized symbols).
For Galileo “Outer Forward Error Correction (FEC2)”, the designers chose to add 60 parity bytes, 15 per parity message. The protected ephemeris should then be smaller than 60 bytes, which is not naively the case - the four existing ephemeris messages total 64 bytes. However, there is some repetition among the four, which allows the formulation of a protected message of only 58 bytes, from which the full 64 bytes can be regenerated.
This leads to a total message of 118 bytes, which is shorter than the 255 byte Reed-Solomon block. To get around this, it is typical to zero-pad an R-S block, and then not transmit the actual zeroes. Further details can be found in my earlier Reed-Solomon page, which also includes running code.
Reed-Solomon can be configured using a lot of parameters, and it is vital to get these right since otherwise nothing works. There is a remarkable gap between the literature and the code here. Reed-Solomon is a very clever piece of mathematics, but it has now been used so long that there are very good libraries available that do the work for you. These libraries require input of concrete parameters. It is however not easy to derive these concrete parameters from the verbose math that many standards publish. With help from expert Daniel Estévez, I found that the following parameters work for Galileo “FEC2”:
- Symbol size in bits: 8
- Number of parity symbols (t or “number of roots”,
nroots): 60 - Padding: 255 - 60 - 58 = 137 bytes
- The extended Galois field generator polynomial coefficients: \(
1 + x^2 +x^3 + x^4 + x^8 \) aka 0x11d (
gfpoly) - The primitive (
prim) element in the Galois field used to generate the Reed Solomon code generator polynomial: 1 - The first consecutive root (
fcr) of the Reed Solomon code generator polynomial: 1
The parameter names match up to the most excellent libfec library.
However, Galileo has (for unknown reasons) added an additional twist: the Reed-Solomon message components get broadcast (individually) in reverse order. Yes.
So, the whole R-S block looks like this, where ‘wt’ stands for ‘word type’, and wt 1 through 4 are the ephemeris itself, and 17 through 20 contain the parity bits.
A few things to note. The Galileo OSS ICD 2.0 explicitly tells you which bytes to lift from the various message types, where you’ll also see that word type 1 is different - unlike the other blocks it includes the IOD and its word type.
The promise of this additional R-S protection is that you can recover the full ephemeris based on any four of the 8 messages. This is indeed true, but there are two things to look out for. If only types 1 through 4 are available, the Reed-Solomon decoder has nothing to work on, so you need to special case that situation.
A second special case to take care of is when word type 1 and three of the parity words are absent. In that case, there would be \( 16 + 3*15 = 61 \) erased symbols, which is 1 more than the FEC2 R-S configuration can recover from. The good news however is that word type 1 starts with two known bytes - a mix of the word type (1) and the IOD. The IOD can be gleaned from any of the other message types. If these two bytes are provided, the R-S decoder can recover the 59 other ones.
Then there is the matter of fragility - the parity words are marked with the two least significant bits from the IOD. This does leave room for ambiguity, especially under conditions of bad reception. Be very careful not to have too long a buffer to gather word types - Reed-Solomon is so good at correcting damage it will happily correct your new ephemeris to the old one!
Secondary Synchronisation Pattern (SSP)
Every two seconds a new Galileo message arrives. Sadly, not all these messages contain a timestamp. We do know they are being transmitted at whole Galileo System Time (GST) seconds though, we just don’t know which second. BeiDou for example transmits a timestamp with each message, but Galileo has been somewhat more frugal with bits.
Through some clever thinking however, it has been found possible to tag each Galileo message (or word) with three different states. These three states are associated with GST time of week MOD 6 being 0, 2 and 4. This state is both represented digitally as the SSP field of a Galileo I/NAV word, but is also visible through the RF modulation. I don’t know enough about this, but the upshot is that a receiver can tell if this is a ‘MOD 0, 2 or 4’ message without having to decode the message itself. And in turn, this is useful under bad signal conditions.
Of note, even receivers that are connected to a cloud-based assisted GPS provider need to know the exact time. Using these three states, a moderately precise clock (+- 3 seconds) can be used to quickly derive an accurate timestamp. In this way, the three timestamp states can contribute even to speeding up the fix of a well connected phone.
Summarising
With these three innovations, unconnected devices will be able to achieve a fix much faster than before. This provides resilience in case of disruptions in connectivity to major cloud providers like Google and Apple. In addition, even when assisted GPS is available, the SSP can help devices to synchronise their clock more quickly.
Further reading
- Galileo OSS ICD 2.0
- Improving the Performance of Galileo E1-OS by Optimizing the I/NAV Navigation Message, Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, Florida, September 2019, pp. 1134-1146, M. Paonni, M. Anghileri, T. Burger, L. Ries, S. Schlötzer, B.E. Schotsch, M. Ouedraogo, S. Damy, E. Châtre, M. Jeannot, J. Godet, D. Hayes
