SkewDB: an open database of GC and other microbial skews
Hello and welcome to this introduction of the SkewDB. This open (downloadable) database contains details of GC skew, plus a dozen other skews, for all 28,000 bacterial chromosomes available through the NCBI genomes service. The database is created using the open source Antonie DNA software. There is also an online viewer that includes graphs.
GC skew is the phenomenon where almost all circular chromosomes tend to have near equal amounts of G and C nucleotides, per strand, but where the leading replication strand contains an excess of G, and the lagging replication strand has an excess of C nucleotides.
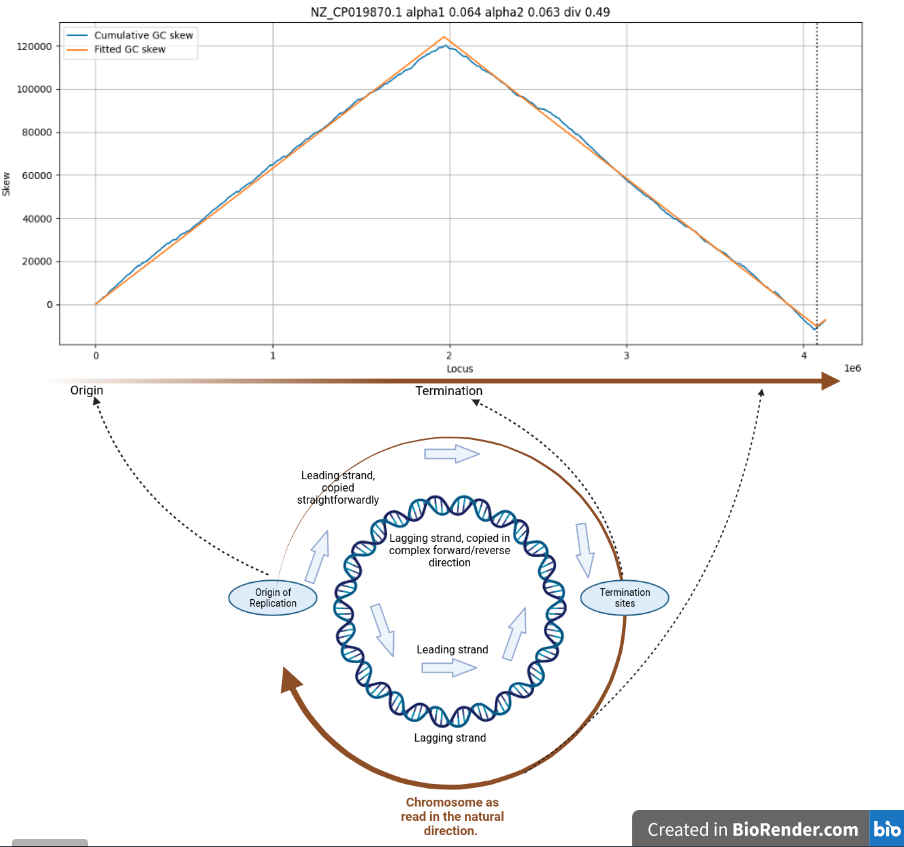
Cumulative GC skew for C. difficile
GC skew was first described in Lobry (1996) and is a very well established phenomenon. It is not very well explained however. As summarised on the Wikipedia “There is lack of consensus in scientific community with regard to the mechanism underlying the bias in nucleotide composition within each DNA strand.”. Why the amounts of G and C nucleotides are very similar (due to Chargaff’s second parity rule) is itself not entirely settled.
Previous work on GC skew includes the SkewIT index of Jennifer Lu and Steven L. Salzberg, and the DoriC database (Hao Luo, Feng Gao). Further references can be found at the end of this page.
I have previously blogged about GC skew here and here. These posts are aimed at a general audience, but despite the informal language, they might serve as a useful (re)introduction to GC skew.
GC skew is very clearly related to the two replication forks travelling in opposite directions in most circular bacterial chromosomes. The skew reverses in polarity at the Origin of replication and at the termination sites.
At these points the replication process switches from simple (5’-3' direction) to the highly complex Okazaki-fragment mediated forward/reverse replication mechanism.
This switch-over is very likely to be among the root causes of GC skew.
In addition, bacteria also show TA skew, and for some phyla this typically occurs in parallel to GC skew (a richness in G is matched by a richness in T). On other phyla, notably Firmicute, TA and GC skew develop in opposite directions.
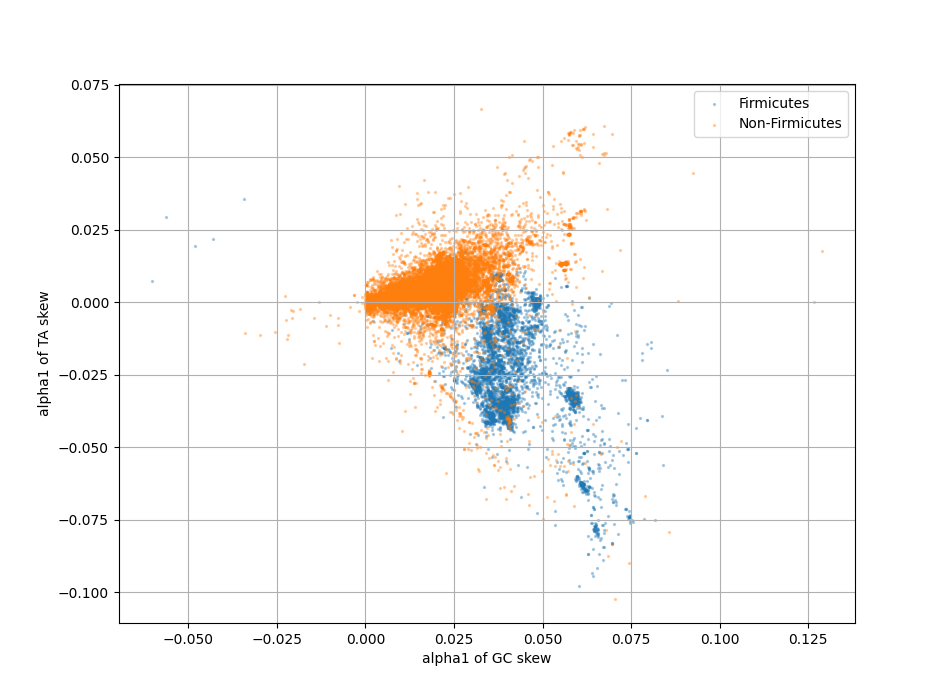
GC versus TA skew direction for 25000 chromosomes
Why GC skew and this database could be useful
Since the distribution of G and C (and T/A) over strands is not well understood, a database providing an overview of the phenomenon can only be helpful.
Looking at the database in silico can be used both to generate and falsify hypotheses.
In addition, a quick look at the SkewDB can also tell us if a chromosome might be mis-assembled, or perhaps consist of multiple chromosomes.
Some possibly interesting observations
Asymmetric GC skew
In this respect it is interesting to note that a sizeable minority of bacteria show highly asymmetric GC skew, with one strand sometimes showing no GC skew at all. There is no obvious explanation at hand how this might happen, given the likely symmetric causes being posited to be behind GC skew. As an example, look at NZ_CP018228.1, NZ_CP072162.1, NZ_CP071399.1, NZ_CP035713.1.
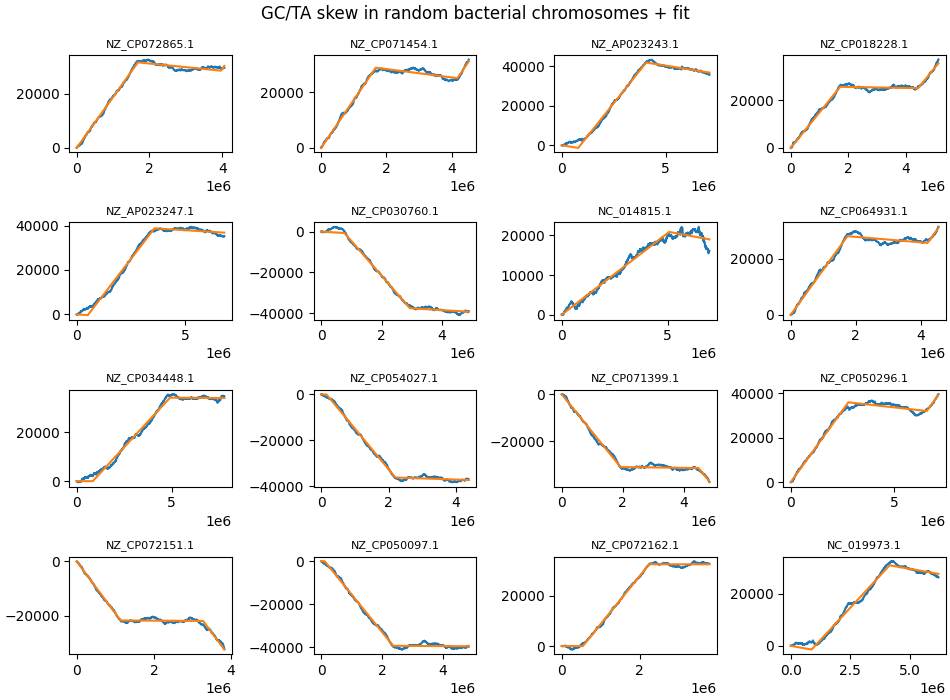
Some random chromosomes where one strand shows no GC skew
The strand bias hypothesis
Many bacteria show a strong strand bias, with genes prefering to live on the leading strand. It is an open question why this happens, but it very clearly does. If genes have an excess of G in their 5’-3’ direction, this would clearly cause GC skew. The excess of genes in the leading strand causes an excess of G’s.
The reverse complemented form is then guaranteed to cause an excess of C’s on the lagging replication strand.
It turns out however that there are many bacteria with no appreciable G/C codon bias, but still showing substantial GC skew. As an example, take a look at NZ_CP032084.1 Achromobacter sp. B7.
In addition, it appears that at least within most individual Firmicutes, local GC skew is influenced by local strand bias, but that there is an independent strand dependent effect. Interestingly this does not happen for TA skew, which can be derived entirely from the strand and codon biases.
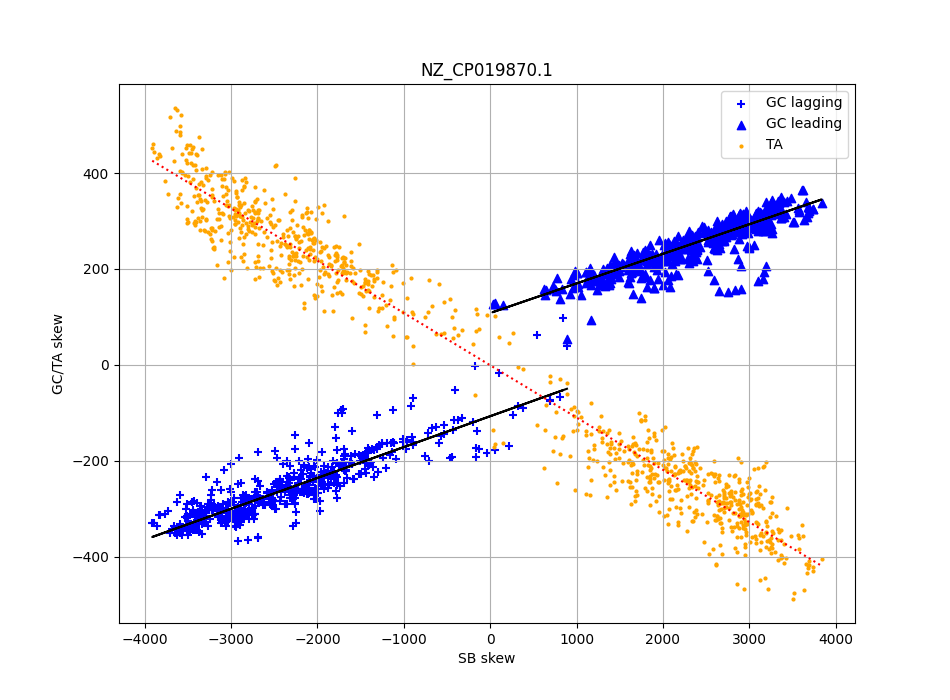
Scatter plot local skew levels (y axis) for C. difficile, and the local gene strand bias
Leading/lagging strand length differences
It appears some chromosomes have a very big discrepancy in lengths between the leading and lagging copying strands. Or in other words, the termination site is not centered. This should be pretty bad for a bacterium, so it might be well worth investigating what is going on.
Some notable examples: NZ_CP016636.1, NC_006512.1, NC_018866.1, NZ_CP058983.1.
Some random chromosomes where the leading/lagging strand length disparity is very large
Part 2 of my informal blog goes into some more detail on these possibly interesting observations.
More details
GC skew and AT skew can be specialised into various sub-skews (skew within genes, skew on non-coding regions, skew on 1st, 2nd and 3rd codon positions). In addition, there is “strand bias” in genes - where more genes tend to be present on the leading replication strand than the lagging replication strand.
The SkewDB contains details of all these skews, both summarised as a single set of number per chromosome, as well as on a 4096-nucleotide basis over each individual chromosome.
On skewdb.org more documentation can be found on where to obtain the SkewDB, and what exactly can be found in there.
